Еще пару слов о квадратурах

Пусть на входе АЦП мы имеем в общем случае сигнал вида:

Где a(t) - изменение амплитуды сигнала, аргумент косинуса - полная фаза.
Поставим ему в соответствие комплексный сигнал:

Сигнал "эс с домиком" вычисляется при помощи преобразования Гильберта и представляет собой идеальный фазовращатель на 90 градусов. Тогда получится, что спектры сигналов S(t) и S^(t) в области положительных частот равны друг другу, а в области отрицательных частот - противоположны. Подробнее об этом возможно позже. Тогда спектр Z(t) будет равен удвоенному спектру S(t) при положительных частотах и равен нулю при отрицательных.
Если дальше раскладывать равенство получится:

Zm(t) получило название комплексной огибающей и представляет исходный сигнал S(t), перенесенный на нулевую частоту.
Рассмотрим комплексную огибающую:

I(t) и Q(t) - квадратурные составляющие, с которыми мы уже знакомы. Подставим полученный результат в формулу для Z(t):

Мы выразили сигнал S(t) через квадратурные составляющие. Что это нам дало? Ну, например, мы можем генерировать квадратуры в диапазоне частот 0..1 МГц и переносить их вверх частотой 1;2;3..N МГц. Гетеродин же

QAM CORDIC

Еще раз пройдемся по наличию. У нас есть метод CORDIC, который для заданной фазы считает квадратурные компоненты I и Q. У нас есть обертки для этого метода, реализующие фазовую, частотную и амплитудную  манипуляцию. Легко заметить, что они очень похожи, поэтому сделать гибрид фазовой и амплитудной манипуляции не составит никакого труда. Называется эта манипуляция квадратурной или QAM. Я буду реализовывать от лени совсем нереальный случай QAM4, когда точки на фазовой плоскости будут располагаться так:

Эта реализация, наверно, нигде не используется, ибо глупая. Но это пример. Код на Verilog выглядит так:

module cordic_qam #(parameter INPUT_CLK = 100000000, parameter INPUT_SAMPLE_RATE = 8000, parameter OUTPUT_SAMPLE_RATE = 10000000) ( input wire clk, input wire en, input wire [ 1 : 0 ] din, output wire [ 19 : 0 ] phase ); localparam SAMPLES_PER_BIT = OUTPUT_SAMPLE_RATE/INPUT_SAMPLE_RATE; localparam PERIODS_PER_BIT = 5; localparam TWO_PI = 524287; localparam PI = 524287>>1; localparam ARG = (TWO_PI * PERIODS_PER_BIT) / SAMPLES_PER_BIT; reg signed [ 31 : 0 ] r_sr = 32'b0; wire signed [ 31 : 0 ] inc_sr = r_sr[31] ? OUTPUT_SAMPLE_RATE : OUTPUT_SAMPLE_RATE-INPUT_CLK; wire signed [ 31 : 0 ] tic_sr = r_sr + inc_sr; wire w_en = ~r_sr[31]; reg r_en = 1'b0; always@(posedge clk) begin r_sr <= tic_sr; r_en <= w_en; end reg [ 19 : 0 ] my_phase = 20'b0; wire [ 19 : 0 ] next_phase = my_phase + ARG; wire [ 19 : 0 ] next_phase_0 = my_phase + (ARG >>> 1); always@(posedge clk) begin if(en) my_phase <= din[0] ? 0 : PI; else if(w_en) begin my_phase <= my_phase + ARG; if(next_phase[19]) my_phase <= next_phase - TWO_PI; end end //cordic delay 14+2 wire signed [ 15 : 0 ] w_re_out; wire signed [ 15 : 0 ] w_im_out; reg [ 15 : 0 ] r_din = 16'b0; always@(posedge clk) r_din <= {r_din[14:0], din[1]}; cordic_phase u0 ( .clk(clk), .arg(my_phase), .Re_out(w_re_out), .Im_out(w_im_out) ); wire [ 15 : 0 ] QAM4 = r_din[15] ? w_im_out : w_im_out >>> 1; assign phase = my_phase; endmodule

И картинка:

Фазовая манипуляция с использованием CORDIC

Был рассмотрен случай частотной манипуляции FSK и амплитудной манипуляции ASK, осталась только фазовая манипуляция. Будет показана обертка для CORDIC для случая BPSK. Если сравнить обертки для разных видов манипуляции, то видно, что они все очень похожи.

module cordic_freq #(parameter INPUT_CLK = 100000000, parameter INPUT_SAMPLE_RATE = 8000, parameter OUTPUT_SAMPLE_RATE = 10000000) ( input wire clk, input wire en, input wire din, output wire [ 19 : 0 ] phase ); localparam SAMPLES_PER_BIT = OUTPUT_SAMPLE_RATE/INPUT_SAMPLE_RATE; localparam PERIODS_PER_BIT = 5; localparam TWO_PI = 524287; localparam PI = 524287>>1; localparam ARG = (TWO_PI * PERIODS_PER_BIT) / SAMPLES_PER_BIT; reg signed [ 31 : 0 ] r_sr = 32'b0; wire signed [ 31 : 0 ] inc_sr = r_sr[31] ? OUTPUT_SAMPLE_RATE : OUTPUT_SAMPLE_RATE-INPUT_CLK; wire signed [ 31 : 0 ] tic_sr = r_sr + inc_sr; wire w_en = ~r_sr[31]; reg r_en = 1'b0; always@(posedge clk) begin r_sr <= tic_sr; r_en <= w_en; end reg [ 19 : 0 ] my_phase = 20'b0; wire [ 19 : 0 ] next_phase = my_phase + ARG; wire [ 19 : 0 ] next_phase_0 = my_phase + (ARG >>> 1); always@(posedge clk) begin if(en) my_phase <= din ? 0 : PI; else if(w_en) begin my_phase <= my_phase + ARG; if(next_phase[19]) my_phase <= next_phase - TWO_PI; end end //cordic delay 14+2 wire signed [ 15 : 0 ] w_re_out; wire signed [ 15 : 0 ] w_im_out; reg [ 15 : 0 ] r_din = 16'b0; always@(posedge clk) r_din <= {r_din[14:0], din}; cordic_phase u0 ( .clk(clk), .arg(my_phase), .Re_out(w_re_out), .Im_out(w_im_out) ); wire [ 15 : 0 ] BPSK = w_im_out; assign phase = my_phase; endmodule

Частотная манипуляция с использованием CORDIC

Продолжаем клепать обертки для CORDIC. Чуток изменяем обертку для ASK и получаем FSK:

module cordic_freq #(parameter INPUT_CLK = 100000000, parameter INPUT_SAMPLE_RATE = 8000, parameter OUTPUT_SAMPLE_RATE = 10000000) ( input wire clk, input wire din, output wire [ 19 : 0 ] phase ); localparam SAMPLES_PER_BIT = OUTPUT_SAMPLE_RATE/INPUT_SAMPLE_RATE; localparam PERIODS_PER_BIT = 5; localparam TWO_PI = 524287; localparam ARG = (TWO_PI * PERIODS_PER_BIT) / SAMPLES_PER_BIT; reg signed [ 31 : 0 ] r_sr = 32'b0; wire signed [ 31 : 0 ] inc_sr = r_sr[31] ? OUTPUT_SAMPLE_RATE : OUTPUT_SAMPLE_RATE-INPUT_CLK; wire signed [ 31 : 0 ] tic_sr = r_sr + inc_sr; wire w_en = ~r_sr[31]; reg r_en = 1'b0; always@(posedge clk) begin r_sr <= tic_sr; r_en <= w_en; end reg [ 19 : 0 ] my_phase = 20'b0; wire [ 19 : 0 ] next_phase = my_phase + ARG; wire [ 19 : 0 ] next_phase_0 = my_phase + (ARG >>> 1); always@(posedge clk) if(w_en) if(din) begin my_phase <= my_phase + ARG; if(next_phase[19]) my_phase <= next_phase - TWO_PI; end else begin my_phase <= my_phase + (ARG >>> 1); if(next_phase_0[19]) my_phase <= next_phase - TWO_PI; end //cordic delay 14+2 wire signed [ 15 : 0 ] w_re_out; wire signed [ 15 : 0 ] w_im_out; reg [ 15 : 0 ] r_din = 16'b0; always@(posedge clk) r_din <= {r_din[14:0], din}; cordic_phase u0 ( .clk(clk), .arg(my_phase), .Re_out(w_re_out), .Im_out(w_im_out) ); wire [ 15 : 0 ] FSK = w_im_out; assign phase = my_phase; endmodule

И картинка:

Амплитудная манипуляция с использованием CORDIC

Амплитудная манипуляция или ASK представляет информационные биты в аналоговый сигнал постоянной частоты с амплитудой, зависящей от значения бита. Так, если уровень кодируется одним битом, то амплитуд соответственно будет 2. Если 2 бита - 4 уровня. CORDIC на Verilog уже отлажен и в него лезть не будем, поэтому будет писать обертку для нашего модуля, реализующие ASK.

module cordic_am #(parameter INPUT_CLK = 100000000, parameter INPUT_SAMPLE_RATE = 8000, parameter OUTPUT_SAMPLE_RATE = 10000000) ( input wire clk, input wire din, output wire [ 19 : 0 ] phase ); localparam SAMPLES_PER_BIT = OUTPUT_SAMPLE_RATE/INPUT_SAMPLE_RATE; localparam PERIODS_PER_BIT = 5; localparam TWO_PI = 524287; localparam ARG = (TWO_PI * PERIODS_PER_BIT) / SAMPLES_PER_BIT; //make OUTPUT_SAMPLE_RATE reg signed [ 31 : 0 ] r_sr = 32'b0; wire signed [ 31 : 0 ] inc_sr = r_sr[31] ? OUTPUT_SAMPLE_RATE : OUTPUT_SAMPLE_RATE-INPUT_CLK; wire signed [ 31 : 0 ] tic_sr = r_sr + inc_sr; wire w_en = ~r_sr[31]; reg r_en = 1'b0; always@(posedge clk) begin r_sr <= tic_sr; r_en <= w_en; end reg [ 19 : 0 ] my_phase = 20'b0; wire [ 19 : 0 ] next_phase = my_phase + ARG; always@(posedge clk) if(w_en) begin my_phase <= my_phase + ARG; if(next_phase[19]) my_phase <= next_phase - TWO_PI; end //cordic delay 14+2 wire signed [ 15 : 0 ] w_re_out; wire signed [ 15 : 0 ] w_im_out; reg [ 15 : 0 ] r_din = 16'b0; always@(posedge clk) r_din <= {r_din[14:0], din}; cordic_phase u0 ( .clk(clk), .arg(my_phase), .Re_out(w_re_out), .Im_out(w_im_out) ); wire [ 15 : 0 ] ASK = r_din[15] ? w_im_out : w_im_out >>> 3; assign phase = my_phase; endmodule

Тут нет ничего не знакомого, кроме счетчика выходной частоты отсчетов. Частота гармонического колебания будет равна INPUT_SAMPLE_RATE*PERIODS_PER_BIT. Чем выше OUTPUT_SAMPLE_RATE, тем больше точек на период. Все завязано на константах, и желательно подбирать их кратными друг другу. В результате получается такая вот картинка:

Улучшаем CORDIC

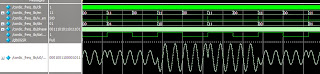
Я улучшил работу модуля на Verilog, причем без особых заморочек. Если смотреть программу на С++, то там наблюдается такая же аномалия. При том она вылезает при повороте на угол 0,03 градуса, при повороте на 0,1 градусов все чисто. Ну что же, первое что приходить на ум - увеличить разрядность фазы, второе что приходит на ум - увеличить количество итераций CORDIC. Сделаем то и другое.

Изначально под фазу было отдано 15 бит, но этого не хватает. Чтобы не было искажений, поставим фазу 20 бит. Количество итераций увеличим с 12 до 14. Тогда график наложения идеального модуля косинуса и рассчитанный CORDIC станет таким:

Текстовые файлы я генерю из С++, т.к. это быстрее. Графики строю в FreeMat. График в окрестностях 0, где был пик относительной погрешности. Поскольку фаза стала 20 битная, то на один период требуется 524287 точек, что очень много. Я ограничился 135000, поэтому будет чуть больше четверти периода. Относительную погрешность буду строить в окрестностях 0, картинка получилась такая:

Пик уменьшился в 5 раз. Считать такую погрешность приемлемой для 16 битного числа или нет решает каждый сам. Если увеличить N до 16, то пик станет равен 4. Вообще в этих точках вот что происходит: вместо правильного числа 0, CORDIC считает -4. Так как на 0 делить мы не можем: вместо 0 ставим 1 и считаем относительную погрешность. Если нужно убрать этот пик - делаем хак. Мы знаем точки, в которых этот выброс, значит при какой-то входном аргументе на выходе ставим 0. По хорошему это уже объединение двух методов: CORDIC и LUT (lookup table). В LUT мы храним значения каких-то углов, а если аргумент попадает между углов LUT, считаем его CORDIC. Я считаю, что -4 вместо 0 не криминал, поэтому оставлю так. В подтверждение своих слов приведу картинку абсолютной погрешности в области около 0:

Отлично, абсолютная погрешность не превышает 6 по модулю, что гораздо лучше 70.

И в заключение еще один хак. Каждую первую итерацию, независимо от угла, мы делаем одинаковое действие: вращаем вектор на 45 градусов. Поэтому мы можем первую итерацию вынести из цикла for, сделав так:

    Re[0] = short(tmp);

    Im[0] = short(tmp);

    int_output_angle = int_angles[0];

    int int_input_angle = my_arg*ARG_N/360.0f;

    for(int k = 0; k < (N-1); k++) {

        if(int_output_angle > int_input_angle) {

            Re[k+1] = Re[k] + (Im[k] >> k+1);

            Im[k+1] = Im[k] - (Re[k] >> k+1);

            int_output_angle -= int_angles[k+1];

        }

        else {

            Re[k+1] = Re[k] - (Im[k] >> k+1);

            Im[k+1] = Im[k] + (Re[k] >> k+1);

            int_output_angle += int_angles[k+1];

        }

    }

Если мы раньше объявляли Re[N+1], то теперь хватит Re[N]. Тогда на Verilog код будем выглядеть так: 

`timescale 1ns / 1ps module cordic_phase( input wire clk, input wire [ 19 : 0 ] arg, output wire [ 15 : 0 ] Re_out, output wire [ 15 : 0 ] Im_out ); localparam N = 14; localparam DAT_WIDTH = 16; localparam ARG_WIDTH = 20; reg signed [ DAT_WIDTH-1 : 0 ] CORDIC_GAIN = 16'd19897; integer k; reg [ ARG_WIDTH-1 : 0 ] angle[0:N-1]; initial begin angle[ 0] = 20'd65536; angle[ 1] = 20'd38688; angle[ 2] = 20'd20441; angle[ 3] = 20'd10376; angle[ 4] = 20'd5208; angle[ 5] = 20'd2606; angle[ 6] = 20'd1303; angle[ 7] = 20'd651; angle[ 8] = 20'd325; angle[ 9] = 20'd162; angle[10] = 20'd81; angle[11] = 20'd40; angle[12] = 20'd20; angle[13] = 20'd10; end reg signed [ DAT_WIDTH-1 : 0 ] Re[0:N-1]; reg signed [ DAT_WIDTH-1 : 0 ] Im[0:N-1]; reg signed [ ARG_WIDTH-1 : 0 ] r_input_arg[0:N-1]; reg signed [ ARG_WIDTH-1 : 0 ] r_output_arg[0:N-1]; reg [ 2 : 0 ] r_quad[0:N-1]; reg signed [ DAT_WIDTH-1 : 0 ] r_Re_out = 16'b0; reg signed [ DAT_WIDTH-1 : 0 ] r_Im_out = 16'b0; always@(posedge clk) begin Re[0] <= CORDIC_GAIN; Im[0] <= CORDIC_GAIN; r_input_arg[0] <= {3'b0, arg[(ARG_WIDTH-4):0]}; r_output_arg[0] <= angle[0]; r_quad[0] <= arg[(ARG_WIDTH-1)-:3]; for(k = 0; k < N-1; k = k + 1) begin if(r_output_arg[k] > r_input_arg[k]) begin Re[k+1] <= Re[k] + (Im[k] >>> k+1); Im[k+1] <= Im[k] - (Re[k] >>> k+1); r_output_arg[k+1] <= r_output_arg[k] - angle[k+1]; r_input_arg[k+1] <= r_input_arg[k]; r_quad[k+1] <= r_quad[k]; end else begin Re[k+1] <= Re[k] - (Im[k] >>> k+1); Im[k+1] <= Im[k] + (Re[k] >>> k+1); r_output_arg[k+1] <= r_output_arg[k] + angle[k+1]; r_input_arg[k+1] <= r_input_arg[k]; r_quad[k+1] <= r_quad[k]; end end r_Re_out <= r_quad[N-1] == 3'b000 ? Re[N-1] : r_quad[N-1] == 3'b001 ? -Im[N-1] : r_quad[N-1] == 3'b010 ? -Re[N-1] : Im[N-1]; r_Im_out <= r_quad[N-1] == 3'b000 ? Im[N-1] : r_quad[N-1] == 3'b001 ? Re[N-1] : r_quad[N-1] == 3'b010 ? -Im[N-1] : -Re[N-1]; end assign Re_out = r_Re_out; assign Im_out = r_Im_out; endmodule