Еще раз пройдемся по наличию. У нас есть метод CORDIC, который для заданной фазы считает квадратурные компоненты I и Q. У нас есть обертки для этого метода, реализующие фазовую, частотную и амплитудную манипуляцию. Легко заметить, что они очень похожи, поэтому сделать гибрид фазовой и амплитудной манипуляции не составит никакого труда. Называется эта манипуляция квадратурной или QAM. Я буду реализовывать от лени совсем нереальный случай QAM4, когда точки на фазовой плоскости будут располагаться так:
Эта реализация, наверно, нигде не используется, ибо глупая. Но это пример. Код на Verilog выглядит так:
Exported from Notepad++
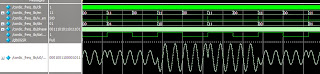
И картинка:
Эта реализация, наверно, нигде не используется, ибо глупая. Но это пример. Код на Verilog выглядит так:
module cordic_qam
#(parameter INPUT_CLK = 100000000, parameter INPUT_SAMPLE_RATE = 8000,
parameter OUTPUT_SAMPLE_RATE = 10000000)
(
input wire clk,
input wire en,
input wire [ 1 : 0 ] din,
output wire [ 19 : 0 ] phase
);
localparam SAMPLES_PER_BIT = OUTPUT_SAMPLE_RATE/INPUT_SAMPLE_RATE;
localparam PERIODS_PER_BIT = 5;
localparam TWO_PI = 524287;
localparam PI = 524287>>1;
localparam ARG = (TWO_PI * PERIODS_PER_BIT) / SAMPLES_PER_BIT;
reg signed [ 31 : 0 ] r_sr = 32'b0;
wire signed [ 31 : 0 ] inc_sr = r_sr[31] ? OUTPUT_SAMPLE_RATE : OUTPUT_SAMPLE_RATE-INPUT_CLK;
wire signed [ 31 : 0 ] tic_sr = r_sr + inc_sr;
wire w_en = ~r_sr[31];
reg r_en = 1'b0;
always@(posedge clk)
begin
r_sr <= tic_sr;
r_en <= w_en;
end
reg [ 19 : 0 ] my_phase = 20'b0;
wire [ 19 : 0 ] next_phase = my_phase + ARG;
wire [ 19 : 0 ] next_phase_0 = my_phase + (ARG >>> 1);
always@(posedge clk)
begin
if(en)
my_phase <= din[0] ? 0 : PI;
else
if(w_en)
begin
my_phase <= my_phase + ARG;
if(next_phase[19])
my_phase <= next_phase - TWO_PI;
end
end
//cordic delay 14+2
wire signed [ 15 : 0 ] w_re_out;
wire signed [ 15 : 0 ] w_im_out;
reg [ 15 : 0 ] r_din = 16'b0;
always@(posedge clk)
r_din <= {r_din[14:0], din[1]};
cordic_phase u0
(
.clk(clk),
.arg(my_phase),
.Re_out(w_re_out),
.Im_out(w_im_out)
);
wire [ 15 : 0 ] QAM4 = r_din[15] ? w_im_out : w_im_out >>> 1;
assign phase = my_phase;
endmodule
И картинка: