Пример ДПФ

Рассмотрим пример умножения тригонометрической функции на комплексную экспоненту.

Рассмотрим сначала функцию косинуса:

Возьмем N = 16, тогда n = [-8, 8). Целое число "4" показывает сколько полных периодов тригонометрической функции лежит в N отсчетах. Спектр такого сигнала:

Спектр симметричен относительно середины и принимает ненулевые значения в точке +- 4. Почему так получается легче всего продемонстрировать в показательной форме, используя формулу Эйлера:

Видно, что косинус представляется двумя комплексными экспонентами с половинной амплитудой и частотами альфа и минус альфа. Для синуса можно проделать те же действия, изменив аргумент на 

Теперь умножим косинус на комплексную экспоненту той же частоты: 

 Получим спектр копию исходного, сдвинутого влево:

При этом видно, что правый пик сдвинулся на нуль. Если перемножить косинус в показательной форме на комплексную экспоненту с одинаковыми частотами, то получится:

Появилось постоянное смещение, равно 1/2. Значение амплитуды получается умножением N = 16 на постоянную составляющую. Так же стоит отметить, что спектр периодичен, потому что 

Рассмотрим пример. Посчитаем 16 точечное ДПФ входной последовательности вида: 

Представим этот сигнал с частой дискретизации 8 кГц, тогда:

При n = 0..15 вычисленные значения:

xin1

[ 1.     0.707  0.    -0.707 -1.    -0.707 -0.     0.707  1.     0.707  

0.    -0.707 -1.    -0.707 -0.     0.707]

xin2

[-0.354 -0.354  0.354  0.354 -0.354 -0.354  0.354  0.354 -0.354 -0.354

  0.354  0.354 -0.354 -0.354  0.354  0.354]

xin

[ 0.646  0.354  0.354 -0.354 -1.354 -1.061  0.354  1.061  0.646  0.354

  0.354 -0.354 -1.354 -1.061  0.354  1.061]

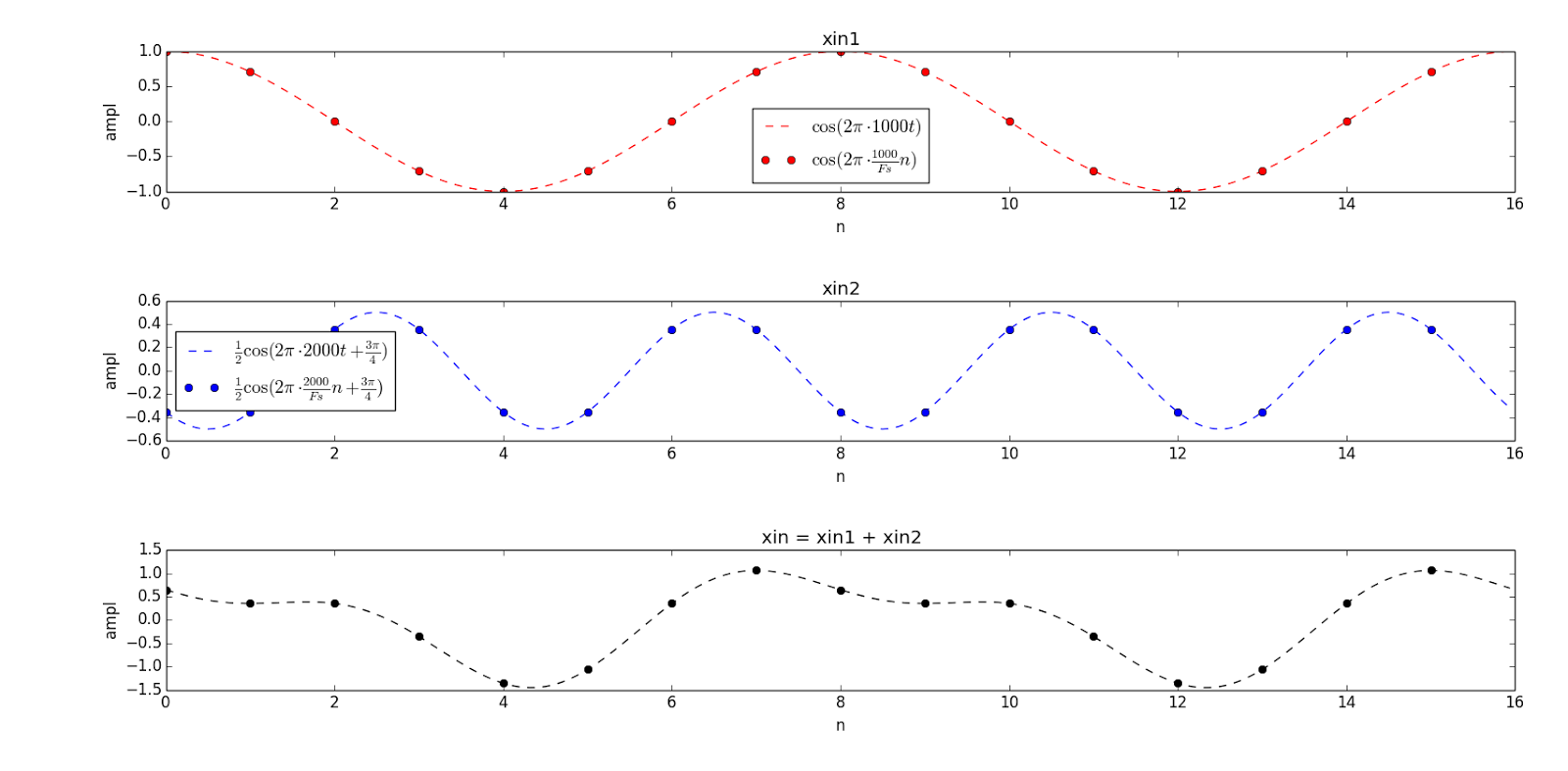
График входного сигнала

Так я считаю ДПФ на Python:

X = np.array([])

for k in range(N):
    csin = np.exp(-1j*2*np.pi*k*n/N)
    X = np.append(X, sum(xin*csin))

X

[ 0.0000+0.j      0.0000+0.j      8.0000+0.j      0.0000+0.j

 -2.8284+2.8284j  0.0000+0.j      0.0000+0.j      0.0000+0.j      0.0000+0.j

  0.0000+0.j      0.0000+0.j      0.0000+0.j     -2.8284-2.8284j

  0.0000+0.j      8.0000+0.j      0.0000+0.j    ]

abs(X)

[ 0.  0.  8.  0.  4.  0.  0.  0.  0.  0.  0.  0.  4.  0.  8.  0.]

180.0*np.angle(X)/np.pi

[   0.    0.    0.    0.  135.    0.    0.    0.    0.    0.    0.    0.

 -135.    0.    0.    0.]

Кросс-компиляция для BeagleBone Black в Eclipse

Простой HOWTO для запуска C++ Hello World проекта в эклипс под Windows.
1. Скачать Eclipse для C/C++ разработчиков. Мой путь: C:\eclipse
2. Скачать Sourcery CodeBench Lite for ARM. Там нужно зарегистрироваться и на почту придет ссылка на скачивание. Установить, например: C:\Sourcery_CodeBench_Lite_for_ARM_GNU_Linux. Переименовать в папке C:\Sourcery_CodeBench_Lite_for_ARM_GNU_Linux\bin cs-make.exe в make.exe и cs-rm.exe в rm.exe.
3. Запустить Eclipse. File - New - C++ Project.
Project type: Hello World C++ Project, Cross GCC. Next-Next-Finish.
4. Project - Properties. C/C++ Build - Settings. Первая вкладка Tool Settings.
Cross Settings - Path: C:\Sourcery_CodeBench_Lite_for_ARM_GNU_Linux\bin
Cross GCC Compiler: arm-none-linux-gnueabi-gcc-4.8.3
Cross G++ Compiler: arm-none-linux-gnueabi-g++
Cross G++ Linker: arm-none-linux-gnueabi-g++
Cross GCC Assemblwe: arm-none-linux-gnueabi-as
OK.
4. Project - Build All. Вывод:
21:15:51 **** Build of configuration Debug for project hello ****
make all
'Building file: ../src/hello.cpp'
'Invoking: Cross G++ Compiler'
arm-none-linux-gnueabi-g++ -O0 -g3 -Wall -c -fmessage-length=0 -MMD -MP -MF"src/hello.d" -MT"src/hello.d" -o "src/hello.o" "../src/hello.cpp"
'Finished building: ../src/hello.cpp'
' '
'Building target: hello'
'Invoking: Cross G++ Linker'
arm-none-linux-gnueabi-g++  -o "hello"  ./src/hello.o
'Finished building target: hello'
' '

21:15:52 Build Finished (took 871ms)
5. Window - Show View - Other... Remote Systems - Remote Systems. В открывшемся окне найти Define a connection to remote system (справа будет рядом со значком minimize/maximize)
Linux -
Host name: 192.168.7.2
Name/Description: BBB
Next. Последовательно выбрать ssh.files, proceses.shell.linux, ssh.shells, ssh.terminals. Finish.
Правой кнопкой по новому соединению - Connect. User ID: root, Password пустой, запомнить User ID, запомнить пароль.
6. Run - Run Configuration... Вкладка С/С++ Remote Application. Двойной щелчок. Connection выбираем BBB.
Remote Absolute Path... : /home/root/{ProjectName}
Commands to execute...: chmod +x /home/root/{ProjectName}. Run
Вывод:
-sh: /usr/bin/led_acc: No such file or directory
root@beaglebone:~# echo $PWD'>'
/home/root>
[1]+  Done(127)               /usr/bin/led_acc
root@beaglebone:~#
root@beaglebone:~# chmod +x /home/root/{ProjectName};/home/root/{ProjectName};ex it
!!!Hello World!!!
logout

снова CORDIC - заключительная

Возвращаюсь к старой теме. Самый хороший результат, который был получен: относительная погрешность = 4 при количество итераций N = 16, при 16-битных значениях квадратур и 20-битном значении фазы. Можно ли улучшить результат? Да. Будем использовать тот же прием, что и при ДПФ.
Абсолютная погрешность при множестве итераций алгоритма CORDIC накапливалась при операции сдвига, где отбрасывалась дробная часть. Да и проблема со сдвигом отрицательной единицы вносила погрешность в расчеты. Поэтому модифицируем алгоритм CORDIC, добавив округление в целочисленную математику.
Я долгое время игрался с сишной моделью и вот результат: main.cpp. На выходе программы имеем консольный вывод разницы для косинуса и синуса между правильным значением и рассчитанном алгоритмом и дисперсию. Дисперсия равна нулю, что, как мне кажется, хорошо.
Я решил сэкономить места в ПЛИС, поэтому урезал точность по фазе до 16 бит, а по составляющим до 14 бит, а количество итераций оставил равным 14.
Графики относительной погрешности для синфазной составляющей:

Графики относительной погрешности для квадратурной составляющей:

Можно еще заметить, что я играл с сочетанием математики с округлением и без. Я искал оптимальное использование того и того, чтобы минимизировать абсолютную погрешность. При этом еще одним фактором минимизации было добиться как можно меньшей величины суммы модулей погрешностей. Если говорить сухими цифрами:

При использовании округления при всех итерациях максимальная погрешность по обеим составляющим равна 6 и нормированная сумма модулей погрешности к числу точек равна 1,160645.

При целочисленной математики значения равны 8 и 1,362732

При оптимальном сочетании значения равны 5 и 0,971802. Графики приведены именно для этого случая.

Ну и переписываем один к одному на verilog: main.v. Получившаяся волна:

Бонус: FFT 2048 на FreeMat
cos = load('cos_delta.txt')/8191;

nfft=2048

X = fft(cos, nfft);

X = X(1:nfft/2);

f = (0:nfft/2-1)*Fs/nfft;

plot(f,mx);

БПФ8 на verilog

От сути БПФ переходим к реализации на Verilog. Я буду писать ДПФ8 с двумя 4-точечными бабочками. Реализация будет полностью параллельной и считать будем за один такт:

Ранее, когда я рассматривал ДПФ4 на примере, была выведена формула для 4-точечной бабочки. Комбинаторная реализация выглядит так:
BF4_comb.v
И тут есть о чем поговорить. Когда рассматривался CORDIC на verilog, вылезла проблема: отрицательные числа и операция сдвига для них. Простой пример, который можно повторить в любом калькуляторе: int(-5) / 2 = -2, int(-5) >> 1 = -3, int(5) / 2 =2, int(5) >> 1 = 2. Результаты по модулю отличаются на единицу в случае сдвига и равны при делении. Как сделать операцию сдвига эквивалентной делению. Прибавить единицу нельзя, потому что int(-5) / 2 = -2, (int(-5) >> 1)  + 1= -2, но int(-4) / 2 = -2 и int(-4) >> 1 = -2. То есть для четных чисел прибавка единицы дает неверный ответ. Ответ оказывается достаточно очевидным: прибавить половину, но половину чего и куда? Половину делителя к исходному числу. Проверка:
Делитель a: 2;
Половина делителя b = a/2;
Сдвиг с = log2(a);
Делимое d = -5;
x = d+b >> c = -5+1 >> 1 = -4 >> 1 = -2. Если подставить любые числа, но равенство не нарушится.
Вопрос: как отразятся изменения на положительные числа? 5 >> 1 = (5 + 1) >> 1  = 3. А это получается округление. Как в школе учили: 2,5 это 3, а 2,2 это 2.

Если посмотреть картинку сверху, то в ней будет одна неточность: чтобы размеры входных данных соответствовали размерам выходных - надо добавить множитель 1/N, то есть по сути усреднить результат. Отсюда сдвиг на 2 вправо для реальной части на четных выходах и по 1 вправо для реальной и мнимой части нечетных выходов.

Раз уж заговорили о размерах входных данных и прочего. Входные данные представлены размерностью 15:0, но по факту данные должны быть 14 битные. Это видно в топовом файле:
FFT8.v
input wire [ 13 : 0 ] din,
Почему так сделано? Во-первых все из-за пресловутых отрицательных чисел. Мы не можем без переполнения умножить максимальное отрицательное числа на -1. Поэтому нужно либо ограничивать входной диапазон от максимального положительного числа до минус максимального положительного, либо на один бит расширять представление числа. Почему я все же расширил представление? Потому что в процессе сложения/умножения мы можем получить число с переполнением, поэтому запаса даже в 1 бит хватит, чтобы в процессе отладки найти проблемное место. Ну и последняя и самая важная причина: выше показано, что мы считаем теперь с округлением, а не отсечением дробной части.

Файл length.v нам уже знаком и служит для вычисления длины гипотенузы. С ним разобрались давно. Вот он считает с отсечением дробной части, что будет видно на результатах тестов.

Осталось только рассмотреть модуль восстановления БПФ8 из ДПФ4. То есть переходим к рассмотрению арифметических операций над комплексными числами. Начнем с умножения: complex_mult.v. Формулу для умножения двух комплексных чисел вспомнит любой, почему прибавляю 512? Потому что потом сдвигаю на 10, или делю на 1024. Почему такая размерность? Я выбрал 12 битные поворачивающие коэффициенты, то есть они могут лежать в диапазоне -2048..2047. Здесь опять же есть вариант ограничить диапазон симметрично -2047..2047, но смысла в этом нет. Дело в том, что модуль поворачивающий множителя всегда равен единице, то есть реальная и мнимая часть лежать в диапазоне -1..1. Чему в целочисленных равна единица? 2047. А чему равен cos(45) ? 1447. Как умножить число на cos(45) в целочисленных? X*1447/2047. Всплыла операция деления. Я хочу изменить деление на сдвиг, потому что делить за один такт сложно. Для этого достаточно диапазон поворачивающих коэффициентов ограничить -1024..1024. Тогда cos(45) = 724, а выражение X*724/1024 можно заменить на X*724 >>> 10.
Сложение комплексных чисел complex_sum.v: все просто и очевидно. Складываем два числа, делим на два, чтобы размерность на выходе была равна размерности числе на входе.
Ну и завершает это все топовый модуль для восстановления БПФ8 block_FFT8.v. В нем задействовано 4 умножителя и 8 сумматоров. По факту мы получим реализацию формулы ДПФ,  деленную на N, где N - количество точек в БПФ.

Промежуточные результаты получены, теперь нужно будет из полностью параллельного БПФ делать конвейер, возможно получится подключить CORDIC, который теперь можно улучшить при помощи приведения операции сдвига к делению для отрицательных чисел.

от ДПФ к БПФ

Прежде чем начать разбираться в БПФ, введем понятия поворачивающего множителя W:

Важно запомнить, что комплексная экспонента со знаком минус, то есть в тригонометрическом виде будет присутствовать cos и -sin, которые будут храниться в памяти. 

Рассмотрим свойства W. Для примера возьмем N = 4. При этом m = 0..N-1.

Получили, что для расчета N коэффициентов W, достаточно посчитать первые N/2 коэффициентов. Это правило справедливо для любого N.

Теперь выведем формулу БПФ с использованием поворачивающего множителя W. Для этого на первом шаге разобьем сумму на две части, выделив четные и нечетные отчеты в две отдельные последовательности.

Получили, что для вычисления N точечного ДПФ достаточно посчитать два N/2 точечных ДПФ из четных и нечетных слагаемых и объединить их. Пользуясь свойствами поворачивающего множителя, можно показать, что для вычисление X(m+N/2) не нужно считать W для него:

Для вычисления X(m+N/2) не нужно ничего считать: достаточно поменять знак поворачивающего множителя  и использовать две суммы, полученные для X(m). 

Итого: для вычисления 8 точечного ДПФ нужно посчитать два 4 точечных ДПФ. Так же можно продолжить и вычислить 4 точечное ДПФ через два 2 точечных.

Далее будем переносить алгоритм на verilog и разбираться во всех тонкостях.

Разбираемся в ДПФ

Дискретное преобразование Фурье - краеугольный камень цифровой обработки сигналов. Формула ДПФ выглядит следующим образом:

N - количество отсчетов ДПФ.

m = 0..N-1 - индекс ДПФ в частотной области.

 n = 0..N-1 - временной индекс входных отсчетов.

x(n) - входные отсчеты во временной области.

X(m) - выходные отсчеты в частотной области.

Начнем, пожалуй, с самого сложного слагаемого в этой сумме:

По формуле Эйлера комплексную экспоненту можно представить как сумму тригонометрических функций. Рассмотрим как меняются индексы m и n при ДПФ.

Рассмотрим пример для N = 4. Формула ДПФ тогда выглядит следующим образом:

Почленно:

X(0) = x(0)*(cos(2*Pi*0*0/4) - jsin(2*Pi*0*0/4))

        + x(1)*(cos(2*Pi*1*0/4) - jsin(2*Pi*1*0/4))

        + x(2)*(cos(2*Pi*2*0/4) - jsin(2*Pi*2*0/4))

        + x(3)*(cos(2*Pi*3*0/4) - jsin(2*Pi*3*0/4)) 

        =

           x(0)*(cos(0*Pi) - jsin(0*Pi))

        + x(1)*(cos(0*Pi) - jsin(0*Pi))

        + x(2)*(cos(0*Pi) - jsin(0*Pi))

        + x(3)*(cos(0*Pi) - jsin(0*Pi))

X(1) = x(0)*(cos(2*Pi*0*1/4) - jsin(2*Pi*0*1/4))

        + x(1)*(cos(2*Pi*1*1/4) - jsin(2*Pi*1*1/4))

        + x(2)*(cos(2*Pi*2*1/4) - jsin(2*Pi*2*1/4))

        + x(3)*(cos(2*Pi*3*1/4) - jsin(2*Pi*3*1/4))

        =

           x(0)*(cos(0*Pi) - jsin(0*Pi))

        + x(1)*(cos(Pi/2) - jsin(Pi/2))

        + x(2)*(cos(Pi) - jsin(Pi))

        + x(3)*(cos(3*Pi/2) - jsin(3*Pi/2))

X(2) = x(0)*(cos(2*Pi*0*2/4) - jsin(2*Pi*0*2/4))

        + x(1)*(cos(2*Pi*1*2/4) - jsin(2*Pi*1*2/4))

        + x(2)*(cos(2*Pi*2*2/4) - jsin(2*Pi*2*2/4))

        + x(3)*(cos(2*Pi*3*2/4) - jsin(2*Pi*3*2/4))

        =

           x(0)*(cos(0*Pi) - jsin(0*Pi))

        + x(1)*(cos(Pi) - jsin(Pi))

        + x(2)*(cos(2*Pi) - jsin(2*Pi))

        + x(3)*(cos(3*Pi) - jsin(3*Pi))

X(3) = x(0)*(cos(2*Pi*0*3/4) - jsin(2*Pi*0*3/4))

        + x(1)*(cos(2*Pi*1*3/4) - jsin(2*Pi*1*3/4))

        + x(2)*(cos(2*Pi*2*3/4) - jsin(2*Pi*2*3/4))

        + x(3)*(cos(2*Pi*3*3/4) - jsin(2*Pi*3*3/4))

        =

           x(0)*(cos(0*Pi) - jsin(0*Pi))

        + x(1)*(cos(3*Pi/2) - jsin(3*Pi/2))

        + x(2)*(cos(3*Pi) - jsin(3*Pi))

        + x(3)*(cos(9*Pi/2) - jsin(9*Pi/2))

Можно заметить, что всегда с входным отсчетом x(0) аргумент комплексной экспоненты равен нулю. При х(1) аргумент равен m*Pi/2. При x(2) - m*Pi, x(3) - m*3*Pi/2. Другими словами: для каждого m-ного выходного отсчета аргумент у тригонометрических функций совершает m - оборотов, причем прирост аргумента величина постоянная и равная 2*Pi*m/N. Какой в этом смысл? Это фактически перенос на нулевую частоту, можно посмотреть здесь как это выводится. Номер выходного отсчета связан с частотой ДПФ выражением:

fs - частота дискретизации сигнала. Так для случая ДПФ4 при частоте дискретизации 4 кГц, анализируемые частоты в спектре будут для X(0) - 0 кГц, X(1) - 1, X(2) - 2, X(3) - 3. Соответственно если смотреть на аргумент у выходных отсчетов, то при X(1) аргумент делает 1 оборот за 4 отсчета, что соответствует 1 кГц. Если не очень понятно, то можно почитать тут подробнее.
Поскольку функция синуса и косинуса периодическая, то для любого аргумента справедливо cos(2*Pi+m) = cos(m). Так же будем пользоваться четностью косинуса и нечетностью синуса. Упростить выражения для выходных отсчетов:

X(0) = x(0) + x(1) + x(2) + x(3) = (x(0) + x(2)) + (x(1) + x(3))

X(1) = x(0)

        + x(1)*(cos(Pi/2) - jsin(Pi/2))

        - x(2)

        + x(3)*(cos(3*Pi/2) - jsin(3*Pi/2))

        =

           x(0) - x(2) + jx(1) -jx(3) = (x(0)-x(2)) - j(x(1)-x(3))

X(2) = x(0)

        - x(1)

        + x(2)

        - x(3)

        =

         (x(0)+x(2))-(x(1)+x(3))

X(3) =  x(0)

        + x(1)*(cos(3*Pi/2) - jsin(3*Pi/2))

        -  x(2)

        + x(3)*(cos(Pi/2) - jsin(Pi/2))

        =

           (x(0) - x(2)) + j(x(1)-x(3)))

Теперь нужно проделать те же действия для N = 8. Получится следующий результат:

Отметим, что входная последовательность с АЦП всегда действительная, поэтому ДПФ симметричен относительно середины: m отсчет ДПФ имеет тот же модуль, что и N-m. Фазовые углы m отсчета равен N-m взятым со знаком минус. Таким образом получается, что пара выходных отсчетов ДПФ m и N-m комплексно сопряжены, но только в случае действительной входной последовательности. Это означает, что в N точечном ДПФ только N/2+1 отсчетов независимы и для вычисления ДПФ достаточно вычислить только их.
Вот простенькая реализация ДПФ на си:

#include <stdio.h> #include <math.h> int const N = 8; void DFT(double * pIN, double * pOUT, int N) { double delta_f = 2*M_PI/N; double RE_out[N]; double IM_out[N]; for(int i = 0; i < N; i++) { RE_out[i] = .0; IM_out[i] = .0; } for(int i = 0; i < N; i++) { for(int j = 0; j < N; j++) { RE_out[i] += *(pIN+j)*cos(delta_f*i*j); IM_out[i] += *(pIN+j)*sin(delta_f*i*j)* -1.0; } *(pOUT+i) = sqrt(RE_out[i]*RE_out[i] + IM_out[i]*IM_out[i]); printf("%d\t\tRE: %5.1f\t IM: %5.1f\tAMPL: %5.1f\n",i, RE_out[i], IM_out[i], *(pOUT+i)); } } int main(){ double * pIN = new double[N]; double * pOUT = new double[N]; for(int i = 0; i < N; i++) { *(pIN+i) = cos(2*M_PI*1*i/N); *(pOUT+i) = .0; } DFT(pIN, pOUT, N); return 0; }

Дальше будем разбираться как посчитать БПФ

Источник синусоидального сигнала

Продолжаем искать применение для CORDIC. Уже была демонстрация различных видов модуляции, теперь сделаем программируемый источник синусоидального сигнала. Программируемым он будет потому, что можно задать частоту выходного сигнала. Генерировать будем и синус, и косинус.

Нам нужно воспроизвести прирост аргумента, равный 2*Pi*f/F, где f - частота выходного сигнала; F - частота дискретизации. Частоту дискретизации возьмем равной 8 кГц, что соответствует одному речевому каналу. Константа 2*Pi для CORDIC была посчитана, операция деления реализована, частота f задается извне. Еще нам понадобятся временные метки, в нашем случае идущие с частотой 8 кГц. Я воспользуюсь бодовым генератором.

Проекты со временем разрастаются, поэтому постепенно я начну переезд на гитхаб. Ну что же, все основные ссылки даны, теперь картинка для привлечения внимания:

Меняем значение на входе out_freq, меняется частота на выходах sin и cos

Какие неявные ограничения есть в такой реализации? Во-первых частота дискретизации равна 8 кГц, это означает, что мы не можем генерировать частоту выше 4 кГц. Частоту повышать будем с помощью интерполирующих фильтров, но об этом потом.

Список интересующих файлов с гитхаба:

cordic_gen.v  - топовый модуль, реализующий логику приращения аргумента для модуля CORDIC.

divider.v - модуль деления с остатком, где делимое 2*Pi*f, делитель F. Смысл остатка для топового модуля следующий: как только счетчик досчитывает до значения остатка от деления, приращение, равное частному, инкрементируется на единицу и счетчик сбрасывается. 

main.v - модуль, реализующий CORDIC. 

Деление на Verilog

Я уже рассматривал операции сложения, вычитания и умножения. Так вышло, что операция деления не является базовой в языке Verilog, поэтому нельзя делить одну регистровую переменную на другую. Сегодня я попытаюсь понять, почему так произошло, и как делить в целочисленных.
Первым делом я начал гуглить этот вопрос и наткнулся на довольно интересную страницу, где описывается умножение и деление на Verilog. Сразу понимания сути это описание не принесло, поэтому стал искать книгу из списка литературы "Computer Organization & Design". И вот в этой книге уже довольно подробно расписано что и почему. Очень советую полистать книгу на досуге.
Сначала определим с чем мы будем иметь дело по ходу работы. У нас будут делимое (divident), делитель (divider), частное (quotient) и остаток (reminder). Причем делимое = делитель*частное + остаток. Для простоты будем рассматривать случай беззнаковых 16 битных целых чисел. Алгоритм выглядит следующим образом:
0. Инициализируем частное = 0. Поскольку каждую итерацию алгоритма делитель нужно будет сдвигать на один разряд вправо, то сделаем 32 битную "копию" делителя, добавив в младшие разряды 16 нулей. Остаток приравниваем к делимому. Дальше весь алгоритм завязан на частном, делителе и остатке. Алгоритм займет N+1 итерацию, где N - количество разрядов делимого и в нашем случае равно шестнадцати.
1. Остаток = остаток - делитель. Если остаток меньше нуля, то вернуть прежний остаток (остаток = остаток + делитель), сдвинуть частное влево на один разряд и в младший разряд подставить 0.
2. Сдвинуть делитель вправо на один разряд. Повторить п. 1.
3..17. Посторить п.2.

Рассмотрим пример из книжки. Поделим 8 битное число 7 на 4 битное число 2.
divident = 7 = 0000 0111;
divider = 2 = 0010;

0. Инициализация:
quotient = 0000;
divider = 0010 0000;
reminder = 0000 0111;

1.
reminder = reminder - divider = 1110 0111 < 0;
reminder = 0000 0111;
quotient = quotient << 1 + 0 = 0000;

2.
divider = divider >> 1 = 0001 0000;
reminder = reminder - divider = 11110111 < 0;
reminder = 0000 0111;
quotient = quotient << 1 + 0 = 0000;

3.
divider = divider >> 1 = 0000 1000;
reminder = reminder - divider = 11111111 < 0;
reminder = 0000 0111;
quotient = quotient << 1 + 0 = 0000;

4.
divider = divider >> 1 = 0000 0100;
reminder = reminder - divider = 0000 0011 > 0;
quotient = quotient << 1 +1 = 0001;

5.
divider = divider >> 1 = 0000 0010;
reminder = reminder - divider = 0000 0001 > 0;
quotient = quotient << 1 +1 = 0011;
end

Алгоритм получается простым, но имеет достаточно много итераций. Вот тут интересная статья про проектирование делителя, в том числе есть простая реализация для случая, когда нужно только частное.

Ну и теперь реализация на Verilog. Количество итераций здесь равно разрядности делимого и получено это благодаря тому, что числа беззнаковые. Благодаря этому можно объединить 0 итерация с 1:

module divider #(parameter N = 32) ( input wire clk, input wire start, input wire [ N-1 : 0 ] divident, input wire [ N-1 : 0 ] divider, output wire [ N-1 : 0 ] quotient, output wire [ N-1 : 0 ] reminder, output wire ready ); localparam M = 2*N; reg signed [ N-1 : 0 ] r_quotient = {N{1'b0}}; assign quotient = r_quotient; reg signed [ M-1 : 0 ] divident_copy = {M{1'b0}}; reg signed [ M-1 : 0 ] divider_copy = {M{1'b0}};; wire signed [ M-1 : 0 ] w_diff = divident_copy - divider_copy; reg [ 5 : 0 ] cnt = 6'b0; assign reminder = divident_copy[N-1:0]; assign ready = cnt == 0; always@(posedge clk) if(ready && start) begin cnt <= 6'd32; r_quotient <= {N{1'b0}}; divident_copy <= {{N{1'b0}}, divident}; divider_copy <= {1'b0, divider, {N-1{1'b0}}}; end else begin cnt <= cnt - 1'b1; divider_copy <= divider_copy >> 1; if(!w_diff[63]) begin divident_copy <= w_diff; r_quotient <= {quotient[30:0], 1'b1}; end else begin r_quotient <= {quotient[30:0], 1'b0}; end end endmodule